证明矩形有两大类四种方法
1、通过角来证明矩形
三个角等于90度的四边形是矩形
一组角为90度的平行四边形是矩形
2、通过对角线来证明矩形
对角线相等且平分的四边形是矩形
对角线相等的平行四边形是矩形
【注意】:判定一个图形是矩形,有四种方法。运用的时候要注意两点:
观察要判定的对象是普通四边形还是平行四边形。这决定这所需添加的条件多少不同。普通四边形添加的条件多,而平行四边形添加的条件少。
用对角线来判定矩形是,“对角线相等且平分的四边形是矩形”的本质就是先判定平行四边形再由对角线相等判定矩形。
二、实战演习
(一)利用一个角为90度的平行四边形是矩形来判定
例1.如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当AB与BC满足什么条件时,四边形EGFH为矩形?并说明理由.
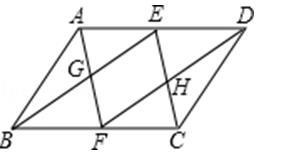
【分析】(1)分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,得到GF∥EH,GE∥FH,则可证四边形EGFH是平行四边形.(2)先证明四边形ABFE是菱形,得到AF⊥BE,即∠EGF=90°,利用一个角为90度的平行四边形为矩形判定。

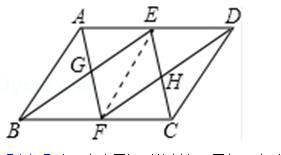
【反思与小结】:第二小问是条件开放性问题,这种题型在思考的时候要从题目的结论入手,得出所需添加的条件。但是在书写证明的时候,要从添加的条件开始证明,证出题目的结论。
例2.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)连接BF,求证:四边形BCAF是矩形.
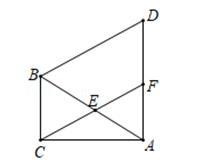
【分析】(1)由△ABC是一个角为60度的直角三角形和△ABD为等边三角形,通过60度的角相等,得到两组平行线,从而得出结论;(2)证出BC=AF,得出四边形BCAF是平行四边形,再由∠ACB=90°,利用一个角为90度的平行四边形为矩形判定四边形BCAF是矩形。

(二)利用对角线相等的平行四边形是矩形来判定
例3.如图,在四边形ABCD中,AD∥BC,AD≠BC,AB∥DE,AF∥DC,E、F两点在BC边上,且BC=3AD.
(1)求证:四边形AEFD是平行四边形.
(2)当AB=DC时,求证:平行四边形AEFD是矩形.
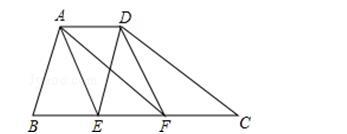
【分析】(1)首先证明四边形ABED和四边形AFCD都是平行四边形,证得AD=BE,AD=FC,从而AD=EF,证明四边形AEFD是平行四边形;
(2)由平行四边形的性质证出DE=AF,再根据对角线相等的平行四边形为矩形证明结论。

【反思与小结】本题的证明自始至终都是借助于平行四边形的证明得到边与边的关系,这是今后我们证明线段之间关系常用的一种方法。
例4.如图,AC、BD相交于点O,且O是AC、BD的中点,点E在四边形ABCD外,且∠AEC=∠BED=90°,求证:四边形ABCD是矩形.
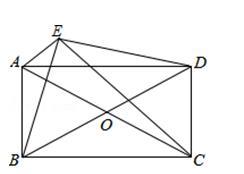
【分析】连接EO,题目已知O为BD和AC的中点,所以四边形ABCD是平行四边形,再由斜边上的中线等于斜边的一半,得到AC=BD,根据对角线相等的平行四边形为矩形证明结论。


【反思与小结】当题目出现直角和中点时,利用斜边上的中线等于斜边的一半是常用方法。如果题目中没有中线,要添加辅助线构造基本图形。
(三)利用三个角为90度的四边形是矩形来判定
例5.如图,AB∥CD,点E、F分别在AB、CD上,连接EF.∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.求证:四边形EGFH是矩形.
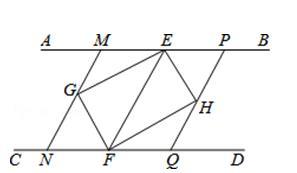
【分析】利用角平分线的定义,根据∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,可以得出∠EHF=90°,∠EGF=90°,∠GEH=90°,利用四边形EGFH是矩形;

【反思与小结】一组同旁内角的角平分线的夹角是90度。一组领补角的角平分线的夹角也为90度。
例6.已知:如图,平行四边形ABCD各角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
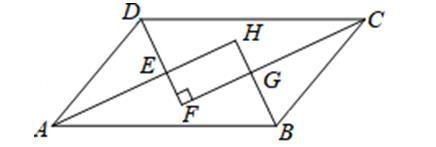
【分析】由于四边形ABCD是平行四边形,那么AD∥BC,利用平行线的性质可得∠DAB ∠ABC=180°,而AH,BH分别平分∠DAB与∠ABC,则∠HAB=∠DAB,∠HBA=∠ABC,那么有∠HAB ∠HBA=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠DEA=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.

【反思与小结】本题的基本思路与例5类似,注意角平分线的应用。
(四)提高训练
例7.如图,在▱ABCD中,AC=8,BD=12,点E、F在对角线BD上,点E从点B出发以1个单位每秒的速度向点D运动,同时点F从点D出发以相同速度向点B运动,到端点时运动停止,运动时间为t秒.
(1)求证:四边形AECF为平行四边形.
(2)求t为何值时,四边形AECF为矩形.
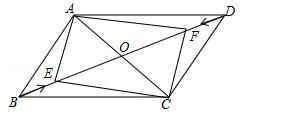
【分析】(1)由对角线可以证明证得四边形AECF为平行四边形;
(2)根据对角线相等的平行四边形是矩形可知,若四边形AECF为矩形,则AC=EF。进而得到方程进行解决。注意要分类讨论。

【反思与小结】动点问题的解决方法通常是找到等量关系列方程解决问题。本题就是由矩形对角线相等来列方程。同时注意动点问题经常用到分类讨论的思想。
三、积累与反思
矩形的证明是初二几何中的重点,同时也是难点之一,与平行四边形、三角形、菱形等知识综合应用,灵活性强,难度大。在初三学习的反比例函数和二次函数中也会形成很多难度较大的题目。所以,牢固掌握基本定理和基本方法还关键所在。
























 扫一扫关注微信
扫一扫关注微信